Huge Lemon的博客

就地逆置线性表元素

2020-01-18

本文分为线性表逆置操作的基本操作和扩展操作

基本操作

顺序表

设计一个高效算法，将顺序表L的所有元素逆置，要求空间复杂度为O(1)

方法一

扫描前半部分元素，对于L.data[i]（0<i<L.length/2），与后半部分对应元素L.data[L.length-i-1].data交换

1
2
3
4
5
6
7
8
void Reverse(SqList &L) {
	ElemType temp;
	for(int i=0;i<L.length/2;i++) {
		temp = L.data[i];
		L.data[i] = L.data[L.length-i-1];
		L.data[L.length-i-1] = temp;
	}
}

方法二

用两个指针i、j分别指向数组的前后

1
2
3
4
5
6
7
8
9
void Reverse(int *a[], int n){
	int i=0, j=n-1, temp;
	While(i<j){
		temp=a[i];
		a[i]=a[j];
		a[j]=temp;
		i++; j--;
	}
}

单链表

逆置链表（带头结点L）用“头插法”。尾插时，最后一个结点的指针要置空。

1
2
3
4
5
6
7
8
9
10
void Reverse(LinkList L) {
	LinkNode *p=L->next, *q;
	L->next=NULL;
	while(p!=NULL){
		q=p->next;
		p->next=L->next;
		L->next=p;
		p=q;
	}
}

双链表

逆置双链表除了上述的步骤外，还多了两个指针，p的后继的前驱和p的前驱的后继

1
2
3
4
5
6
7
8
9
10
11
12
13
void Reverse(DLinkList L) {
	DLinkNode *p=L->next, *q;
	L->next=NULL;
	while(p!=NULL){
		q=p->next;
		p->next=L->next;
		if(p->next!=NULL)  //第一个用“头插法”插入L的结点没有后继
			P->next->prior=p;
		L->next=p;
		p->prior=L;
		p=q;
	}
}

扩展操作

两个顺序表位置互换

一维数组A[m+n]中一次存放两个线性表(a1, a2, …, am)和(b1, b2 , …, bn)。编写一个算法，将数组中两个线性表的位置互换—>(b1,b2,…,bn, a1,a2,…,am)

算法思想：将A[m+n]中全部元素逆置为(bn, bn-1, …, b2, b1, am, am-1, …, a2, a1)，再对前n个元素和后m个元素分别逆置

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void Reverse(int A[], int left, int right, int arraySize){
	//逆置(aleft, aleft+1, …, aright)
	if(left>=right||right>=arraySize)
		return;
	int mid=(left+right)/2;
	for(int i = 0;  i<= mid - left; i++){
		//这里i作为下标的增量
		int temp=A[left+i];
		A[left+i]=a[right-i];
		A[right-i]=temp;
	}
}
void Exchange(int A[], int m, int n, int arraySize){
	//数组A[m+n]中，从0到m-1存放顺序表(a1,a2,…,am)，从m到n-1存放(b1,b2,…,bn)
	Reverse(A, 0, m+n-1, arraySize);
	Reverse(A, 0, n-1, arraySize);
	Reverse(A, n, m+n-1, arraySize);
}

三个顺序表位置互换

设规模n=3m, m≥1的顺序表存储在一维数组int array[n]中，它含有的元素为(a1,a2,…,am, b1, b2 , …, bm,c1,c2,…,cm)。请编写算法将上述顺序表改造成为(c1,c2,…,cm, bm, …, b2, b1, a1,a2,…,am)，要求时间复杂度和空间复杂度尽可能低。

1
2
3
4
5
6
7
8
9
10
11
12
13
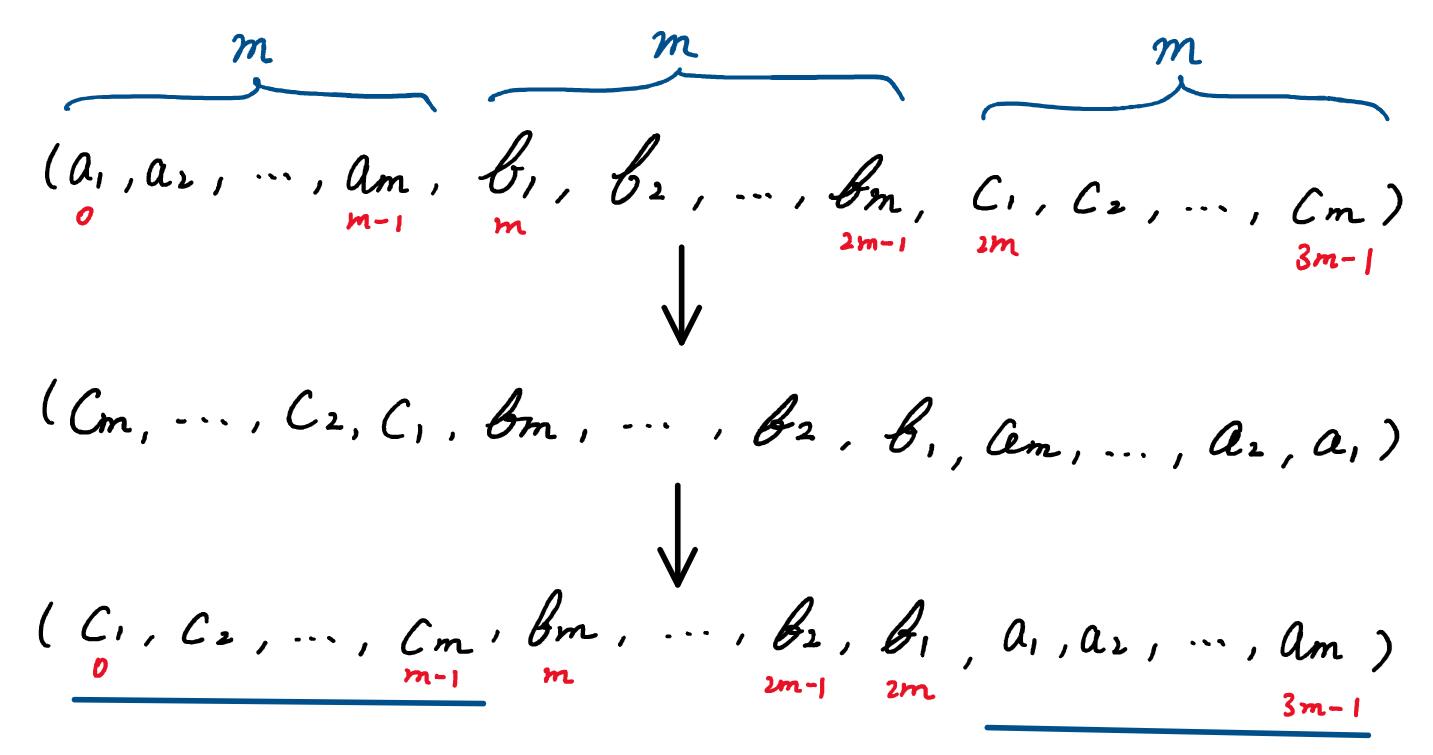
14
void Reverse(int array[], int left, int right) {
	int temp, mid, i;  //i作为下标增量
	mid = (left+right)/2;
	for(i = 0; i <= mid - left; i++){
		temp=a[left+i];
		a[left+i]=a[right-i];
		a[right-i]=temp;
	}
}
void Exchange(int array[], int m){
	Reverse(array, 0, 3m-1);
	Reverse(array, 0, m-1);
	Reverse(array, 2m, 3m-1);
}

总结

就地逆置线性表元素基本操作总结为“二分交换”，基本思想是从头开始将前半部分与后半部分以中心元素对称的元素进行交换，直到走到了中心元素位置

Tags: 算法 LeetCode
← 文件控制块与索引节点的总结 二叉树的应用 →
赏
使用支付宝打赏
使用微信打赏

若你觉得我的文章对你有帮助，欢迎点击上方按钮对我打赏